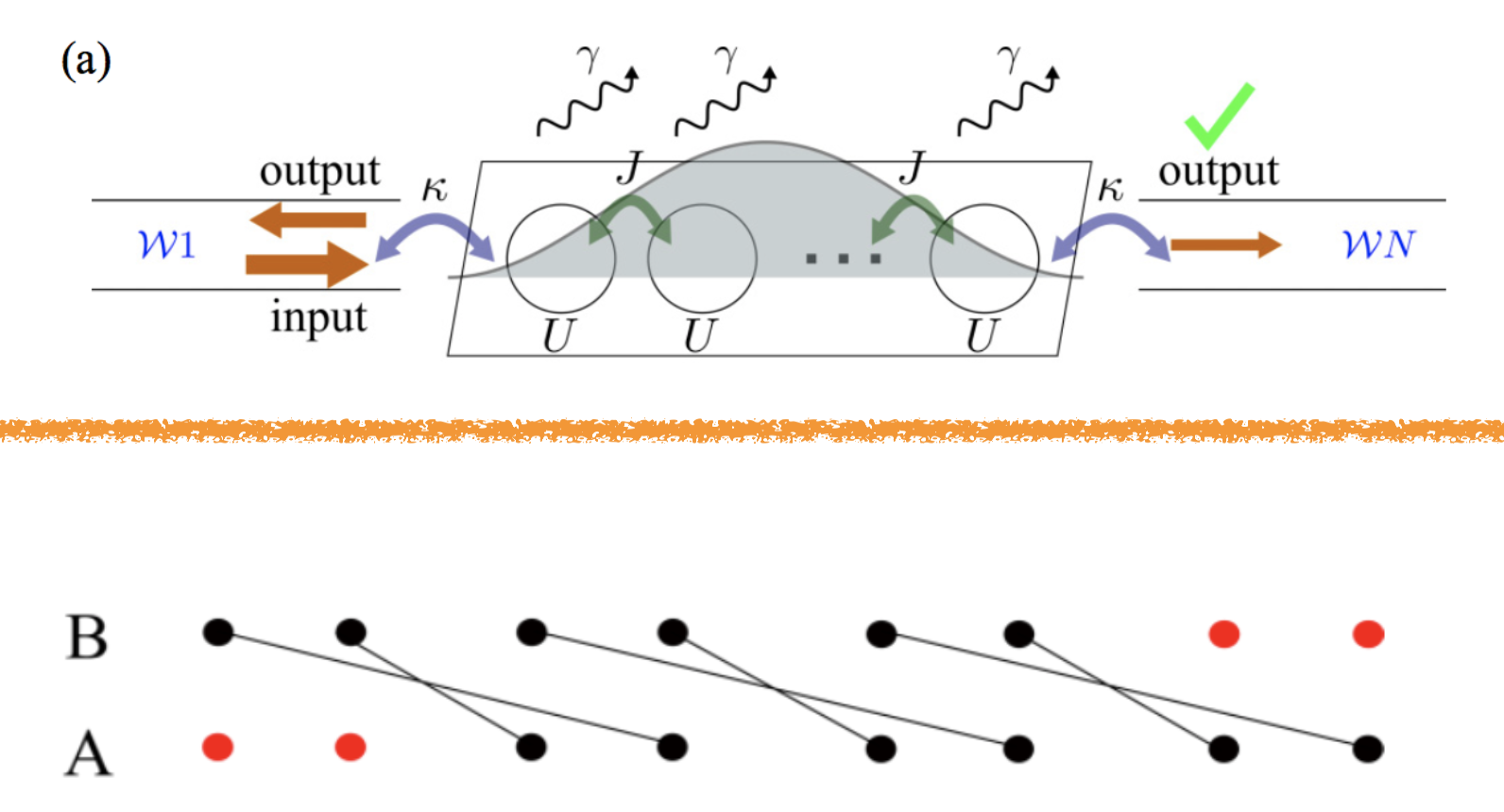
Strongly correlated photon transport in a nonlinear photonic lattice with the disorder: Probing signatures of the localization transition
T. F. See, V. M. Bastidas, J. Tangpanitanon, D. G. Angelakis
Phys. Rev. A. 99, 033835 (2019) [PDF]
We study the transport of few-photon states in open disordered nonlinear photonic lattices. More specifically, we consider a waveguide quantum electrodynamics (QED) setup where photons are scattered from a chain of nonlinear resonators with on-site Bose-Hubbard interaction in the presence of an incommensurate potential. Applying our recently developed diagrammatic technique that evaluates the scattering matrix (S matrix) via absorption and emission diagrams, we compute the two-photon transmission probability and show that it carries signatures of the underlying localization transition of the system. We compare the calculated probability to the participation ratio of the eigenstates and find close agreement for a range of interaction strengths. The scaling of the two-photon transmission probability suggests that there might be two localization transitions in the high energy eigenstates corresponding to interaction and quasiperiodicity respectively. This observation is absent from the participation ratio. We analyze the robustness of the transmission signatures against local dissipation and briefly discuss possible implementation using current technology.
Detection of topological phases by quasilocal operators
W. C. Yu, P.D. Sacramento, Y. Chao, D. G. Angelakis, Hai-Qing Lin
Phys. Rev. B 99, 115113 (2019) [PDF]
It was proposed recently by some of the authors that the quantum phase transition of a topological insulator like the Su-Schrieffer-Heeger (SSH) model may be detected by the eigenvalues and eigenvectors of the reduced density matrix. Here we further extend the scheme of identifying the order parameters by considering the SSH model with the addition of triplet superconductivity. This model has a rich phase diagram due to the competition of the SSH “order” and the Kitaev “order,” which requires the introduction of four order parameters to describe the various topological phases. We show how these order parameters can be expressed simply as averages of projection operators on the ground state at certain points deep in each phase and how one can simply obtain the phase boundaries. A scaling analysis in the vicinity of the transition lines is consistent with the quantum Ising universality class.