Quantum Computing and Quantum Technologies

The ability to control individual quantum systems in customised setups and materials, is paving the way for a quantum second revolution where the fundamental notions of quantum superposition and quantum entanglement will be an integral part of the inner workings of operational quantum devices. These will include  quantum computers and simulators, quantum sensors and quantum communication systems. 

In our group we are working in all aspects of quantum technologies, from the basic science behind them all the way to simulating and helping to develop operating quantum devices. Our special interest is in quantum simulation and quantum computation. In this direction, we study and develop novel quantum algorithms implementable in a variety of quantum platforms including superconducting quantum circuits, slow light, and integrated photonic chips.

   Current main research threads

Recent projects:

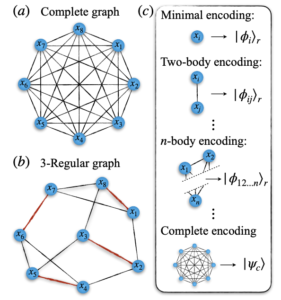
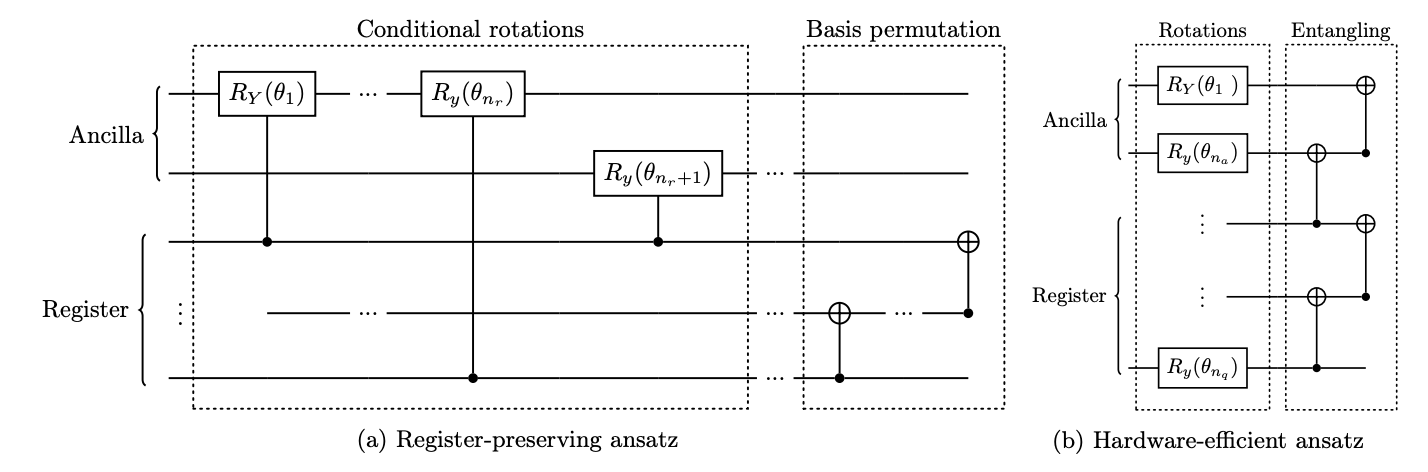
Qubit-efficient encoding schemes for binary optimisation problems (Quantum 5, 454, 2021)

Doing binary optimization problems either via quantum annealing or QAOA require as many qubits as in the classical variables. Realistic quadratic optimization problems (QUBO) usually entail 10.000 classical variables which means current approaches using NISQ devices are very far from achieving anything of real application (Google for example recently managed to barely do 23 qubits for a MaxCut 3-regular graph).  In our first work we are proposing a set of novel variational quantum algorithms for QUBO  where  n classical variables can be implemented on O(log n) number of qubits. Our encoding scheme allows for a systematic increase in correlations among the classical variables captured by a given quantum state by progressively increasing the number of qubits. We apply this minimal encoding to find approximate solutions of a general problem instances comprised of 64 classical variables using 7 qubits. Next, we show how two-body correlations can be incorporated in the variational quantum state and how it can improve the quality of the approximate solutions. We give examples by solving a 42-variable Max-Cut problem using only 8 qubits where we exploit the specific topology of the problem. We analyze whether these cases can be optimized efficiently given the limited resources available in state-of-the-art quantum platforms. Lastly, we present the general framework for extending the expressibility of the probability distribution to any multi-body correlations.

Qubit efficient quantum algorithms for the vehicle routing problem on quantum computers of the NISQ era (https://arxiv.org/abs/2306.08507, 2023)

The vehicle routing problem with time windows (VRPTW) is a classic optimization problem that arises in many different areas, such as logistics and transportation. The goal of the VRPTW is to find the shortest possible route for a fleet of vehicles to visit a set of destinations. In recent years, there has been growing interest in using variational quantum algorithms (VQAs), to find approximate solutions to problems that can be formulated as quadratic unconstrained binary optimization (QUBO) problems. In this work, we formulate the VRPTW as a QUBO and apply a quantum variational approach to the VRPTW using our earlier suggested encoding scheme described in [Tan et al., Quantum 5, 454 (2021)] to reduce drastically the number of qubits required. We evaluate our approach on a set of VRPTW instances ranging from 11 to 3964 routes constructed with data provided by researchers from ExxonMobil. We compare the solutions obtained with standard full encoding approaches for which the max problems size possible in NISQ era are of the order of 20-30 routes. We run our algorithms in simulators as well as cloud quantum hardware provided by IBMQ, AWS (Rigetti) and IonQ and benchmark our results against each other as well as on the simulators. We show that our approach can find approximate solutions to the VRPTW that are comparable to the solutions found by quantum algorithms using the full encoding. Our results suggest that our unique encoding approach, provides a promising approach to drastically reducing the number of qubits required to find decent approximate solutions for industry-based optimization problems.

Landscape approximation of low energy solutions to binary optimization problems (https://arxiv.org/abs/2307.02461, 2023)

We show how the localization landscape, originally introduced to bound low energy eigenstates of disordered wave media and many-body quantum systems, can form the basis for hardware-efficient quantum algorithms for solving binary optimization problems. Many binary optimization problems can be cast as finding low-energy eigenstates of Ising Hamiltonians. First, we apply specific perturbations to the Ising Hamiltonian such that the low energy modes are bounded by the localization landscape. Next, we demonstrate how a variational method can be used to prepare and sample from the peaks of the localization landscape. Numerical simulations of problems of up to 10 binary variables show that the localization landscape-based sampling can outperform QAOA circuits of similar depth, as measured in terms of the probability of sampling the exact ground state.

Exponential Qubit Reduction in Optimization for Financial Transaction Settlement (https://arxiv.org/abs/2307.07193, 2023)

We extend the qubit-efficient encoding presented in [Tan et al., Quantum 5, 454 (2021)] and apply it to instances of the financial transaction settlement problem constructed from data provided by a regulated financial exchange. Our methods are directly applicable to any QUBO problem with linear inequality constraints. Our extension of previously proposed methods consists of a simplification in varying the number of qubits used to encode correlations as well as a new class of variational circuits which incorporate symmetries, thereby reducing sampling overhead, improving numerical stability and recovering the expression of the cost objective as a Hermitian observable. We also propose optimality-preserving methods to reduce variance in real-world data and substitute continuous slack variables. We benchmark our methods against standard QAOA for problems consisting of 16 transactions and obtain competitive results. Our newly proposed variational ansatz performs best overall. We demonstrate tackling problems with 128 transactions on real quantum hardware, exceeding previous results bounded by NISQ hardware by almost two orders of magnitude.

Recent experimental advances strongly suggest that noisy intermediate-scale quantum (NISQ) devices with few hundred quantum nodes/qubits are soon to be available. In principle, these devices can outperform classical computers in particular tasks by exploiting their intractably large Hilbert space, achieving the so-called quantum supremacy. Demonstrating quantum supremacy and efficient machine learning tasks in digital quantum circuits has recently attracted tremendous interests both experimentally and theoretically and become a promising candidate towards the first real-world application of near-term quantum computing. In this thread we explore how analog based quantum processors implemented in different quantum many-body platforms such as cold ion, atoms and superconducting chips can also be used to benchmark and demonstrate such tasks and have complementary abilities to purely digital approaches.

Recent projects

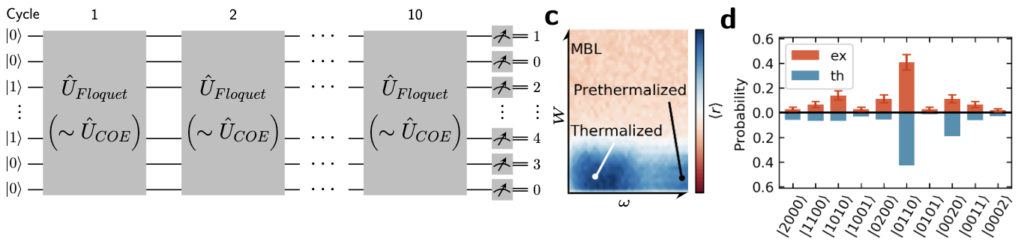
Efficiently Extracting Multi-Point Correlations of a Floquet Thermalized System (https://arxiv.org/abs/2210.08556, Oct 2022)

Our joint work with the leading group of Prof. JW Pan in China on quantum supremacy in many-body systems is out in the arXiv! Our theory prediction from last year that driven many-body systems can be shown to be hard to sample from, has been verified in a beautiful experiment with cold atoms in lattices!

Quantum supremacy in driven quantum many-body systems (https://arxiv.org/abs/2002.11946)

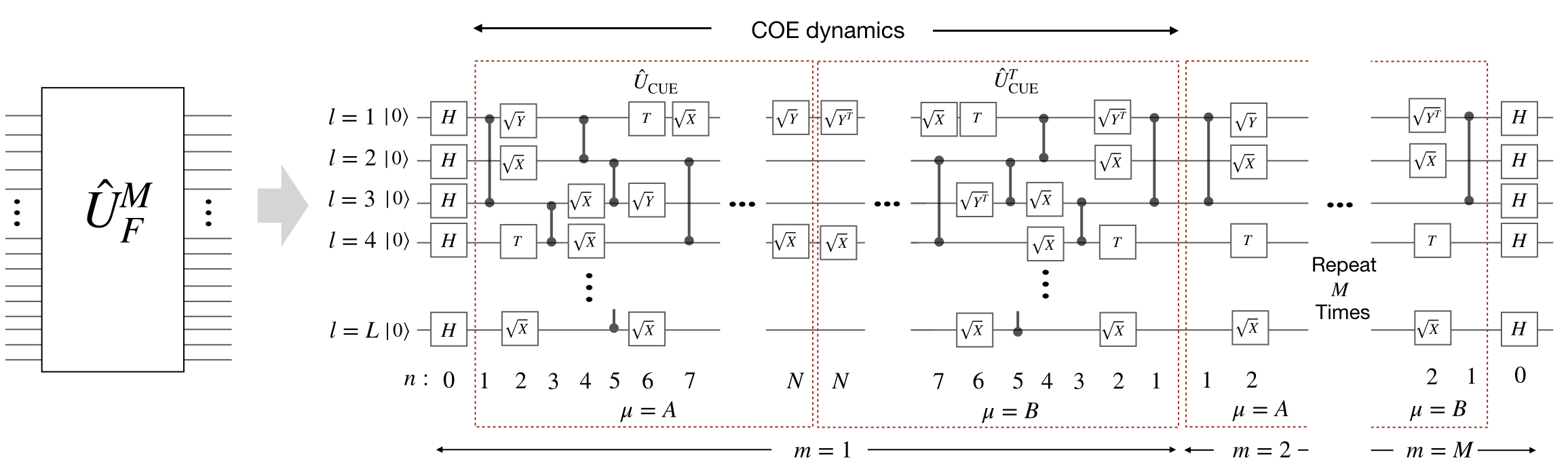We show that quantum supremacy can be obtained in generic periodically-driven quantum many-body systems. Our analysis is based on the eigenstate thermalization hypothesis and strongly-held conjectures in complexity theory. To illustrate our work, We give examples of simple disordered Ising chains driven by global magnetic fields and Bose-Hubbard chains with modulated hoppings. Our proposal opens the way for a large class of quantum platforms to demonstrate and benchmark quantum supremacy.

Expressibility and trainability of parameterized analog quantum systems for machine learning applications (PRR 2, 043364, 2020 )

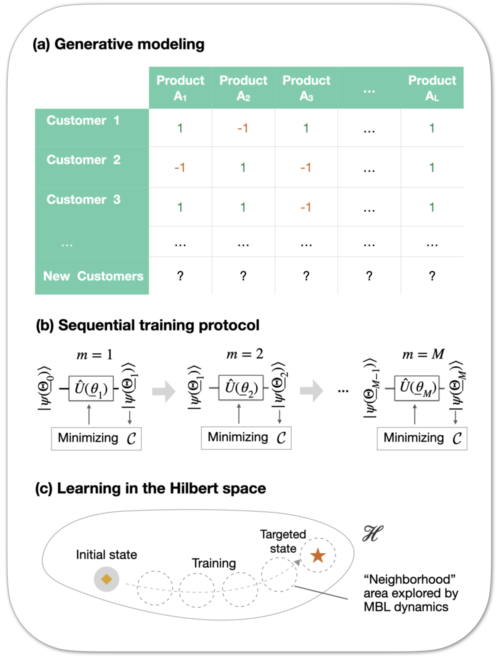Parameterized quantum evolution is the main ingredient in variational quantum algorithms for near-term quantum devices. In digital quantum computing, it has been shown that random parameterized quantum circuits are able to express complex distributions intractable by a classical computer, leading to the demonstration of quantum supremacy. However, their chaotic nature makes parameter optimization challenging in variational approaches. Evidence of similar classically-intractable expressibility has been recently demonstrated in analog quantum computing with driven many-body systems. A thorough investigation of trainability of such analog systems is yet to be performed. In this work, we investigate how the interplay between external driving and disorder in the system dictates the trainability and expressibility of interacting quantum systems. We show that if the system thermalizes, the training fails at the expense of the a large expressibility, while the opposite happens when the system enters the many-body localized (MBL) phase. From this observation, we devise a protocol using quenched MBL dynamics which allows accurate trainability while keeping the overall dynamics in the quantum supremacy regime. Our work shows the fundamental connection between quantum many-body physics and its application in machine learning. We conclude our work with an example application in generative modeling employing a well studied analog many-body model of a driven Ising spin chain. Our approach can be implemented with a variety of available quantum platforms including cold ions, atoms and superconducting circuits

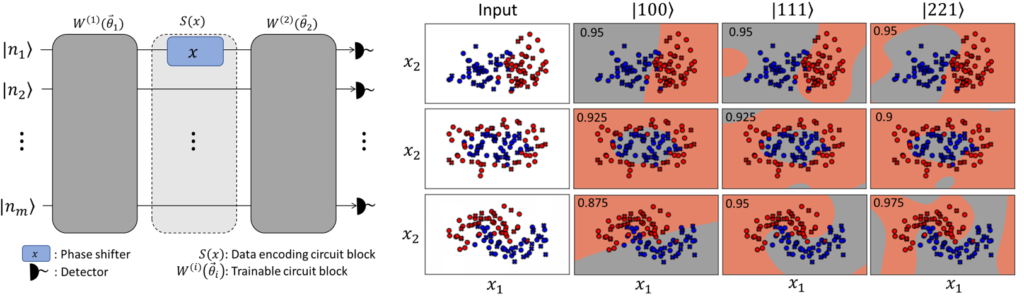Recent projects Fock State-enhanced Expressivity of Quantum Machine Learning Models. (EPJ Quantum Technology 9 (1), 16) The data-embedding process is one of the bottlenecks of quantum machine learning, potentially negating any quantum speedups. In light of this, more effective data-encoding strategies are necessary. We propose a photonic-based bosonic data-encoding scheme that embeds classical data points using fewer encoding layers and circumventing the need for nonlinear optical components by mapping the data points into the high-dimensional Fock space. The expressive power of the circuit can be controlled via the number of input photons. Our work shed some light on the unique advantages offers by quantum photonics on the expressive power of quantum machine learning models. By leveraging the photon-number dependent expressive power, we propose three different noisy intermediate-scale quantum-compatible binary classification methods with different scaling of required resources suitable for different supervised classification tasks.

Recent projects

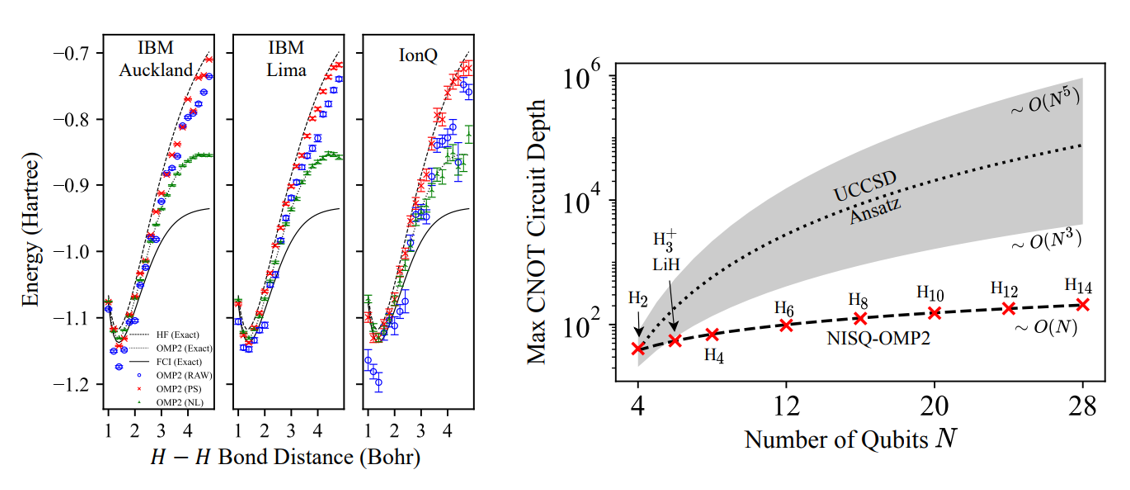
Computing Electronic Correlation Energies using Linear Depth Quantum Circuits. ( arXiv:2207.03949)

Efficient computation of molecular energies is an exciting application of quantum computers, but current noisy intermediate-scale quantum (NISQ) devices can only execute shallow circuits, limiting existing quantum algorithms to small molecules. Here we demonstrate a variational NISQ-friendly algorithm for computing electronic correlation energies perturbatively, trading deep circuits in exchange for more shallow circuits with depth linear in the number of qubits. We tested the algorithm on several small molecules, both with classical simulations including noise models and on cloud quantum processors, showing that it not only reproduces the equilibrium molecular energies but it also captures the perturbative electronic correlation effects at longer bond distances. As fidelities of quantum processors continue to improve our algorithm will enable the study of larger molecules compared to existing approaches with higher-order polynomial circuit depth.

Classical computers require enormous computing power and memory to simulate even the most modest quantum systems. That makes it difficult to model, for example, why certain materials are insulators and others are conductors or even superconductors. R. Feynman had grasped this since the 1980s and suggested to use instead another more controllable and perhaps artificial quantum system as a “quantum computer” or specifically in this case a “quantum simulator”. Quantum simulators include cold atom and ions, photons, polaritons as well as strongly interacting photonic systems such as those found in superconducting circuit QED. Strong interacting photons can be used to implement quantum simulations and many-body physics where photonic excitation plays the main role with complementary properties to cold atom and ion approaches such as more accessible measurements and access to open driven dissipative phenomena. We have been active is this area from the early proposals on equilibrium models of Mott transitions to the more recent works in driven dissipative platforms as well as in experiments in collaboration with experimental groups. Example recent projects: Spectroscopic signatures of many-body localization with interacting photons in superconducting qubits (theory and experiment, Science 2017) Statistical mechanics is founded on the assumption that a system can reach thermal equilibrium, regardless of the starting state. Interactions between particles facilitate thermalization, but, can interacting systems always equilibrate regardless of parameter values. The energy spectrum of a system can answer this question and reveal the nature of the underlying phases. However, most experimental techniques only indirectly probe the many-body energy spectrum. Using a chain of nine superconducting qubits, we implement a novel technique for directly resolving the energy levels of interacting photons. We benchmark this method by capturing the intricate energy spectrum predicted for 2D electrons in a magnetic field, the Hofstadter butterfly. By increasing disorder, the spatial extent of energy eigenstates at the edge of the energy band shrink, suggesting the formation of a mobility edge. At strong disorder, the energy levels cease to repel one another and their statistics approaches a Poisson distribution – the hallmark of transition from the thermalized to the many-body localized phase. Our work introduces a new many-body spectroscopy technique to study quantum phases of matter.   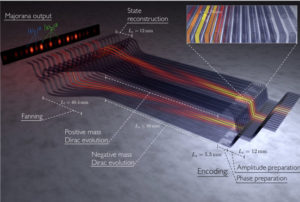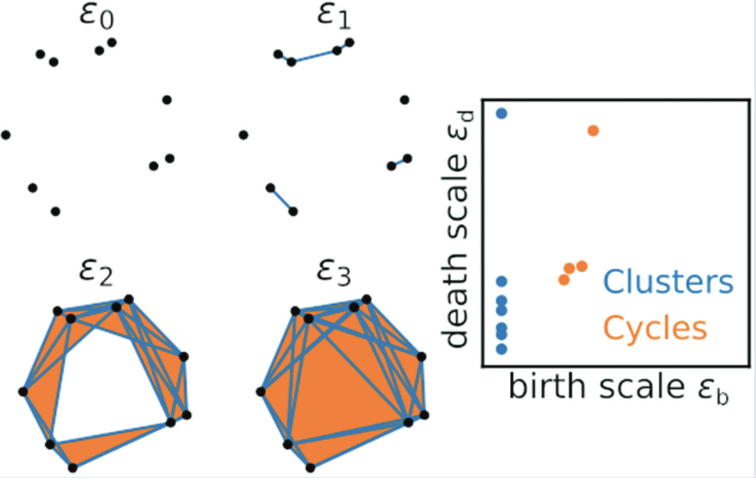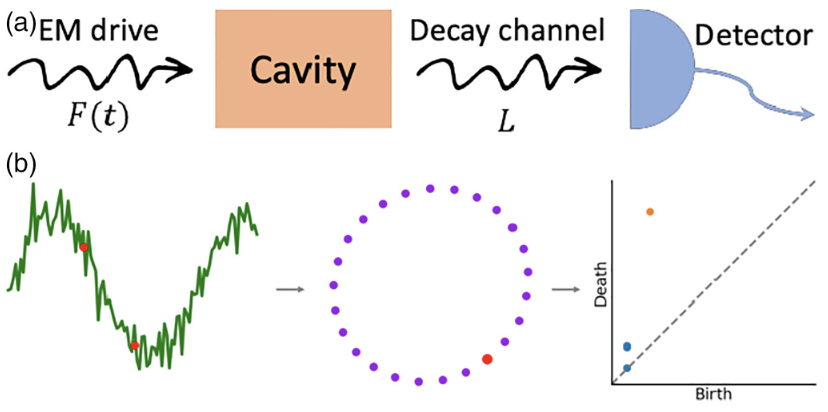Optical simulation of charge conservation violation and Majorana dynamics in integrated photonic chips (Theory ac experiment, Optica 2015) Forbidden physics has been seen in an experiment – sort of. Here in  collaboration with the Szameit group in Germany,  we simulated with light the behaviour of an impossible particle of the Majorana equation, we name the  “Majoranon…” Unphysical solutions are ruled out in physical equations, as they lead to behavior that violates fundamental physical laws. One of the celebrated equations that allows unphysical solutions is the relativistic Majorana equation, thought to describe neutrinos and other exotic particles predicted in theories beyond the standard model. The neutrally charged Majorana fermion is the equation’s physical solution, whereas the charged version is, due to charge nonconservation, unphysical and cannot exist. Here, we present an experimental scheme simulating the dynamics of a charged Majorana particle by light propagation in a tailored waveguide chip. Specifically, we simulate the free-particle evolution as well as the unphysical operation of charge conjugation. We do this by exploiting the fact that the wave function is not a directly observable physical quantity and by decomposing the unphysical solution to observable entities. Our results illustrate the potential of investigating theories beyond the standard model in a compact laboratory setting.

Topological data analysis refers to approaches for systematically and reliably computing abstract ‘shapes’ of complex data sets. In a recent work, we present a topological pipeline for characterizing quantum dynamics, which draws inspiration from the classical approach by using single quantum trajectory unravelings of the master equation to construct analog quantum attractors and extract their topology using persistent homology. We apply the method to a periodically modulated Kerr nonlinear cavity to discriminate parameter regimes of regular and chaotic phases using limited measurements of the system.

Recent projects:

Topological data analysis and machine learning
(Advances in Physics: X, 8, 2202331, 2023)

Topological data analysis refers to approaches for systematically and reliably computing abstract ‘shapes’ of complex data sets. There are various applications of topological data analysis in life and data sciences, with growing interest among physicists. We present a concise review of applications of topological data analysis to physics and machine learning problems in physics including the unsupervised detection of phase transitions. We finish with a preview of anticipated directions for future research.

Unravelling quantum chaos using persistent homology
(Phys. Rev. E 107, 044204, 2023)

In this paper, we present a topological pipeline for characterizing quantum dynamics, which draws inspiration from the classical approach by using single quantum trajectory unravelings of the master equation to construct analog quantum attractors and extract their topology using persistent homology. We apply the method to a periodically modulated Kerr-nonlinear cavity to discriminate parameter regimes of regular and chaotic phases using limited measurements of the system.

Topological physics can greatly assist the design of advanced quantum systems and devices. Topological states are naturally protected against disorder and dissipation and can be used for a variety of tasks in quantum technologies.

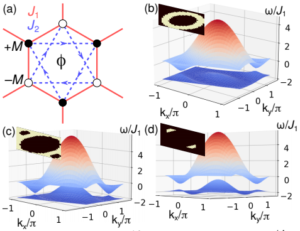Photonic band structure design using persistent homology (APL Photonics 2021)

The machine learning technique of persistent homology classifies complex systems or datasets by computing their topological features over a range of characteristic scales. There is growing interest in applying persistent homology to characterize physical systems such as spin models and multiqubit entangled states. Here, we propose persistent homology as a tool for characterizing and optimizing band structures of periodic photonic media. Using the honeycomb photonic lattice Haldane model as an example, we show how persistent homology is able to reliably classify a variety of band structures falling outside the usual paradigms of topological band theory, including “moat band” and multi-valley dispersion relations, and thereby control the properties of quantum emitters embedded in the lattice. The method is promising for the automated design of more complex systems such as photonic crystals and Moiré superlattices.
 

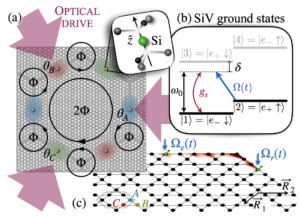Quantum state transfer via acoustic edge states in a 2D optomechanical array (NJP 2020)

We propose a novel hybrid platform where solid-state spin qubits are coupled to the acoustic modes of a two-dimensional array of optomechanical nano cavities. Previous studies of coupled optomechanical cavities have shown that in the presence of strong optical driving fields, the interplay between the photon-phonon interaction and their respective inter-cavity hopping allows the generation of topological phases of sound and light. In particular, the mechanical modes can enter a Chern insulator phase where the time-reversal symmetry is broken. In this context, we exploit the robust acoustic edge states as a chiral phononic waveguide and describe a state transfer protocol between spin qubits located in distant cavities. We analyze the performance of this protocol as a function of the relevant system parameters and show that a high-fidelity and purely unidirectional quantum state transfer can be implemented under experimentally realistic conditions. As a specific example, we discuss the implementation of such topological quantum networks in diamond based optomechanical crystals where point defects such as silicon-vacancy centers couple to the chiral acoustic channel via strain.

Thouless pumping of quantum states of interacting bosons (PRL 2016)

We have recently put forward a scheme that can reliably transport quantum states of a few photons along a line of miniature quantum circuits. More specifically we show how to implement topological or Thouless pumping of interacting photons in one-dimensional nonlinear resonator arrays by simply modulating the frequency of the resonators periodically in space and time. The interplay between the interactions and the adiabatic modulations enables robust transport of Fock states with few photons per site. We analyze the transport mechanism via an effective analytic model and study its topological properties and its protection to noise. We conclude by a detailed study of an implementation with existing circuit-QED architectures.


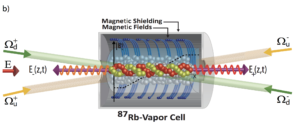
Probing topological relativistic models with slow light in room temperature  (https://arxiv.org/abs/1711.09346)

Here we use a slow light quantum light-matter interface at room temperature to implement an analog simulator of complex relativistic and topological physics. In collaboration with the SUNY group of Eden Figureoa, we have realized the famous Jackiw-Rebbi model (JR), the celebrated first example where relativity meets topology. Our system is based upon interacting dark state polaritons (DSP’s) created by storing light in a rubidium vapor using a dual-tripod atomic system and is based in our earlier theory proposal in 2014. The DSP’s temporal evolution emulates the physics of Dirac spinors and is engineered to follow the JR regime by using a linear magnetic field gradient. We also probe the obtained topologically protected zero-energy mode by analyzing the time correlations between the spinor components. Our implementation paves the way towards quantum simulation of more complex phenomena involving many quantum relativistic particles.

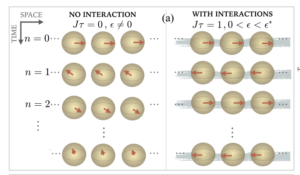Discrete time crystal in globally driven interacting quantum systems without disorder (PRA 2019)

Time crystals in periodically driven systems have initially been studied assuming either the ability to quench the Hamiltonian between different many-body regimes, the presence of disorder or long-range interactions. Here we propose the simplest scheme to observe discrete time crystal dynamics in a one-dimensional driven quantum system of the Ising type with short-range interactions and no disorder. The system is subject only to a periodic kick by a global magnetic field, and no extra Hamiltonian quenching is performed. We analyze the emerging time crystal stabilizing mechanisms via extensive numerics as well as using an analytic approach based on an off-resonant transition model. Due to the simplicity of the driven Ising model, our proposal can be implemented with current experimental platforms including trapped ions, Rydberg atoms, and superconducting circuits.

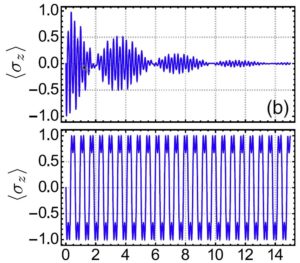Driven open quantum systems and floquet stroboscopic dynamics (PRL 2016)

” Pity poor Schrodinger’s cat”. As if it weren’t enough to wish a cat into a state of being simultaneously dead and alive, physicists now have an idea for how to keep it that way – and the answer is to shake it. ….”
Read more from the CQT highlight for non specialists “Shaking Schrodinger’s cat may protect it from the environment”

Abstract: We provide an analytic solution to the problem of system-bath dynamics under the effect of high-frequency driving that has applications in a large class of settings, such as driven-dissipative many-body systems. Our method relies on discrete symmetries of the system-bath Hamiltonian and provides the time evolution operator of the full system, including bath degrees of freedom, without weak-coupling or Markovian assumptions. An interpretation of the solution in terms of the stroboscopic evolution of a family of observables under the influence of an effective static Hamiltonian is proposed, which constitutes a flexible simulation procedure of nontrivial Hamiltonians. We instantiate the result with the study of the spin-boson model with time-dependent tunneling amplitude. We analyze the class of Hamiltonians that may be stroboscopically accessed for this example and illustrate the dynamics of system and bath degrees of freedom.

Colloquium Talk (July 2017)

10th year anniversary of CQT

Collaborations