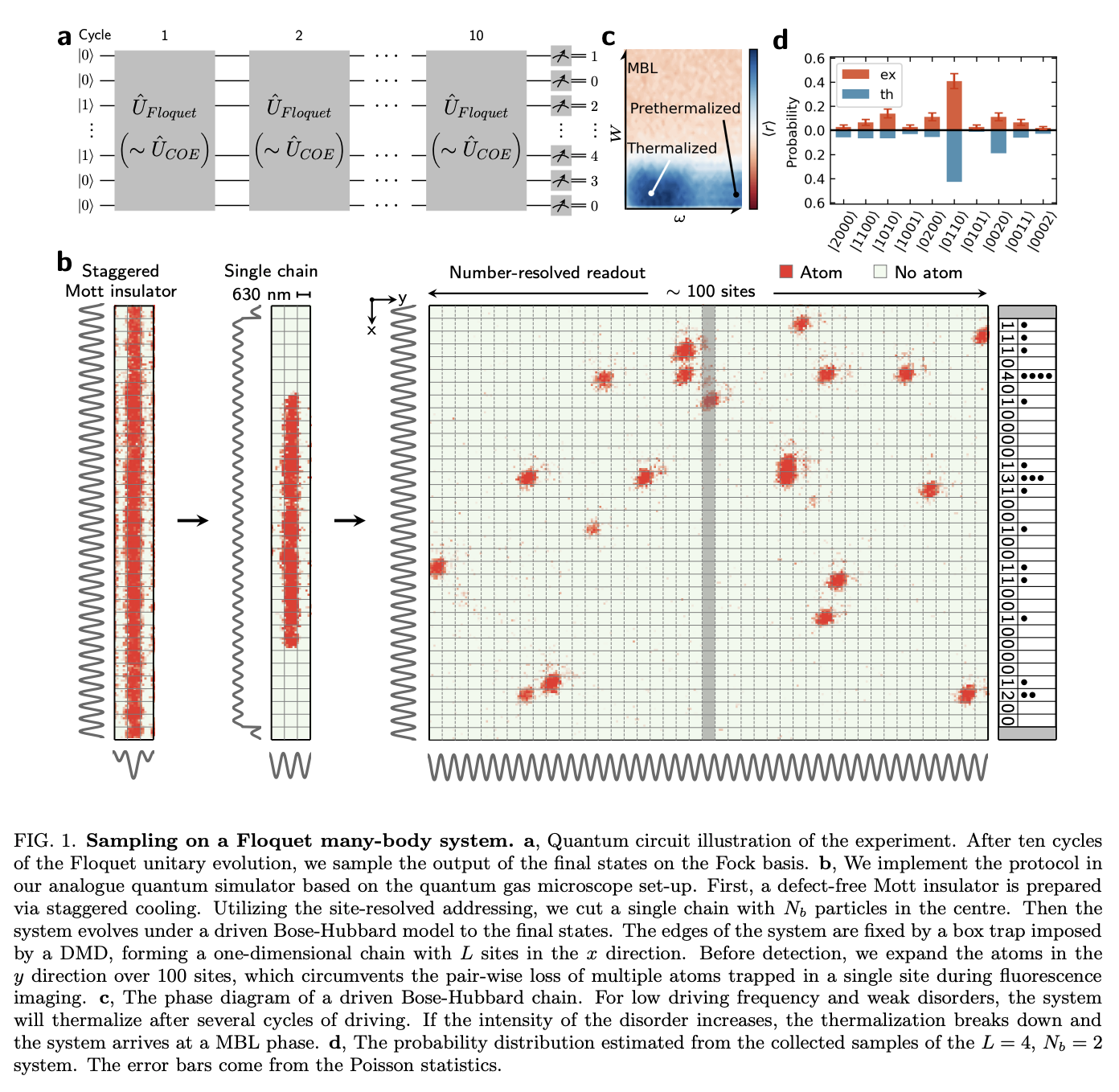
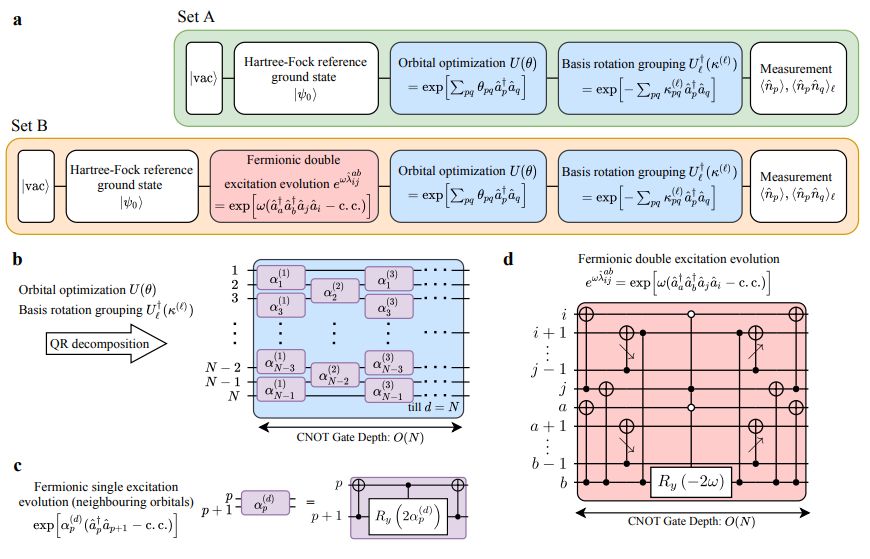
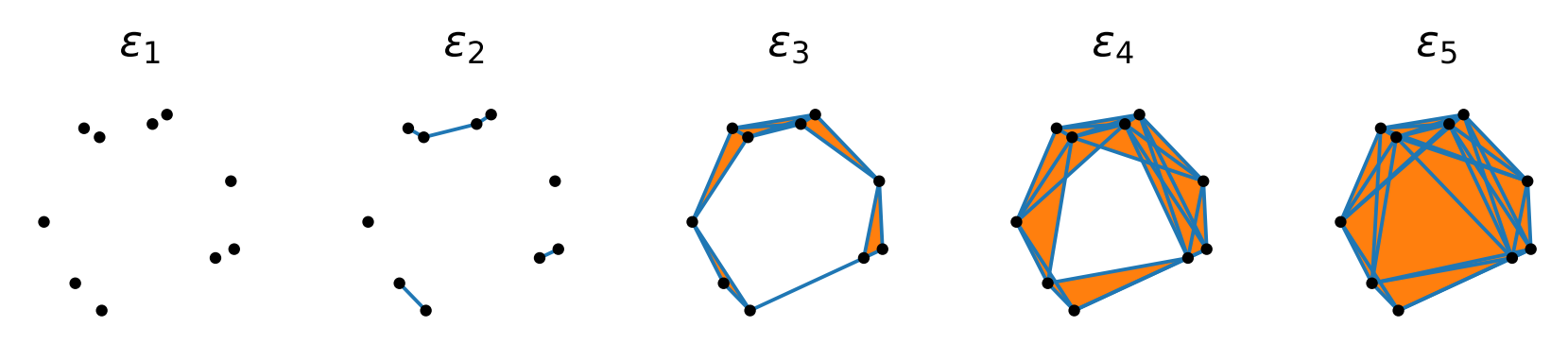
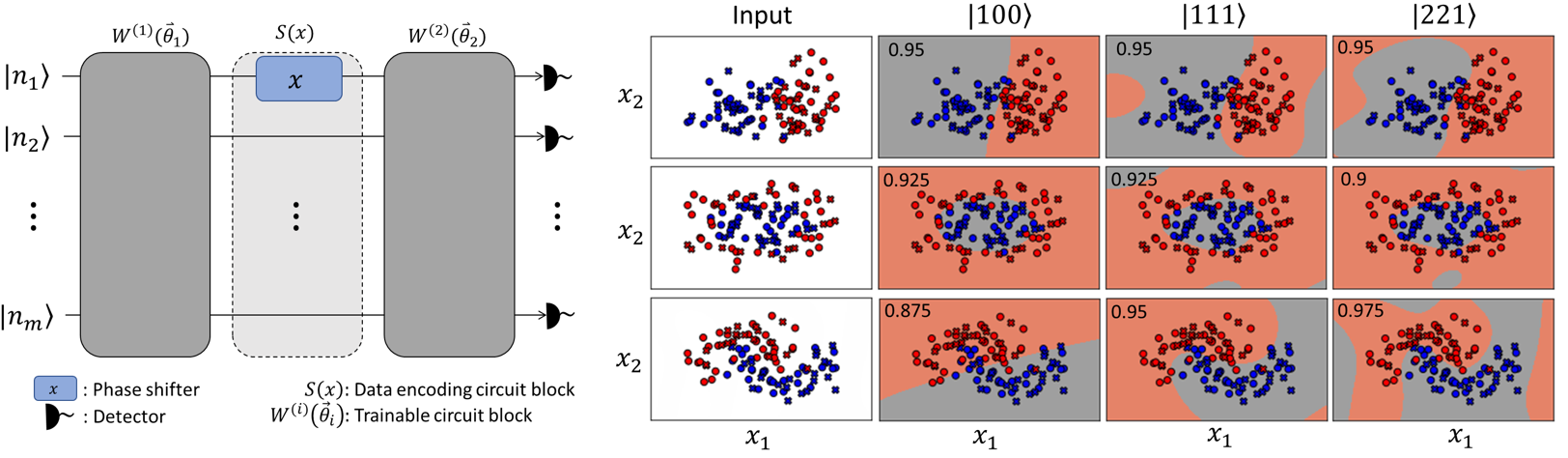
Qubit efficient quantum algorithms for the vehicle routing problem on quantum computers of the NISQ era
Ioannis D. Leonidas, Alexander Dukakis, Benjamin Tan, Dimitris G. Angelakis
arXiv:2306.08507
The vehicle routing problem with time windows (VRPTW) is a classic optimization problem that arises in many different areas, such as logistics and transportation. The goal of the VRPTW is to find the shortest possible route for a fleet of vehicles to visit a set of destinations. In recent years, there has been growing interest in using variational quantum algorithms (VQAs), to find approximate solutions to problems that can be formulated as quadratic unconstrained binary optimization (QUBO) problems. In this work, we formulate the VRPTW as a QUBO and apply a quantum variational approach to the VRPTW using our earlier suggested encoding scheme described in [1] to reduce drastically the number of qubits required. We evaluate our approach on a set of VRPTW instances ranging from 11 to 3964 routes constructed with data provided by researchers from ExxonMobil. We compare the solutions obtained with standard full encoding approaches for which the max problems size possible in NISQ era are of the order of 20-30 routes. We run our algorithms in simulators as well as cloud quantum hardware provided by IBMQ, AWS (Rigetti) and IonQ and benchmark our results against each other as well as on the simulators. We show that our approach can find approximate solutions to the VRPTW that are comparable to the solutions found by quantum algorithms using the full encoding. Our results suggest that our unique encoding approach, provides a promising approach to drastically reducing the number of qubits required to find decent approximate solutions for industry-based optimization problems.